Current and Ongoing Research Projects
Dr. Andreas Aristotelous
- (Invited Special Session Talk) Modeling Dorsal Closure, AIMS 2016 Meeting, Orlando, FL, July 2016.
- Organizer for Special Session at AMS Fall Southeastern Sectional Meeting, NCSU, November 2016.
- Poster Presentation Prize awarded for “Numerical study of biofilm growth in a microgravity
environment,” at SIAM Mathematics of Planet Earth conference, PA, September 2016.
Aristotelous, A. C., Klapper, I., Grabovsky, Y., Pabst, B., Pitts, B. and Stewart, P. S. (2015) Diffusive Transport Through Host-Biofilm Systems. Phys. Rev. E , 92-2, 022703.
Description: Many host-biofilm systems, consist of heterogeneous mixtures of aggregates of microbes intermixed with host material. A key property is analyzed, namely reactive depletion, in such systems and is argued that two regimes are possible: (1) a homogenizable mixture of biofilm and host that in important ways acts effectively like a homogeneous macrobiofilm and (2) a distribution of separated microbiofilms within the host with independent local microenvironments.
Aristotelous, A. C., Karakashian, O. A. and Wise, S. M. (2015) Adaptive, Second-Order in Time, Primitive-Variable Discontinuous Galerkin Schemes for a Cahn-Hilliard Equation with a Mass Source. IMA J. Numer. Anal., 35-3, 1167—1198.
Description: Two fully discrete, discontinuous Galerkin schemes with time-dynamic, locally refined meshes in space are developed for a fourth-order Cahn–Hilliard equation with an added nonlinear reaction term, a phenomenological model that can describe cancerous tumour growth. Proofs of stability and convergence with optimal-order error bounds, have been presented, even in the case where the spatial mesh is changing with time.
The following is a description of an ongoing project with Duke Mathematics and Biology lab group:
Dorsal closure is a part of the Drosophila embryogenesis. It constitutes a model for cell sheet morphogenesis during development and wound healing. For this reason the study of the various mechanisms governing dorsal closure is of great importance. Here we strive to devise a flexible modeling platform employing individual based techniques that will allow us to incorporate experimental data and give us the freedom to test different kinds of modeling equations on the various parts of the simulated Drosophila embryo.
Additional projects are described on Dr. Aristotelous's page, which will be updated regularly.
Dr. Allison Kolpas
The paper “Consequences of mating and predation risk for longevity in a freshwater snail: abstinence
makes the heart beat longer” by J.R. Auld, A. D. Helker, and A. Kolpas was published on September 22, 2016 in
the Journal of Evolutionary Biology. (Adam Helker is a computational mathematics major in the 3-2 applied and computational math program.)
“Spotlight on Research Award” -- October 2016
Optimal Mating Strategies
NSF RUI grant in Evolutionary Ecology. Award No. DEB-1406231.
Title: “A theoretical and experimental investigation of optimal mating strategies
in a hermaphrodite", co-PI with Dr. Josh Auld (Biology), WCUPA July 1, 2014-June 30,
2017.
C. Stratton, A. Kolpas, and J. Auld, Optimal Mating Strategies for Preferentially Outcrossing Simultaneous Hermaphrodites
in the Presence of Predators, in preparation.
Description: A mathematical model is developed to understand the life-history evolution of hermaphroditic snails that can alter their allocation to and timing of reproduction in response to mate availability and predators. The strategy that optimizes fitness (contribution to the gene pool) is found under a variety of scenarios and compared with experimental findings.
Macroinvertebrate dispersal
K. E. Anderson, L. E. Harrison, R. M. Nisbet, and A. Kolpas. Modeling the influence of flow on invertebrate drift across spatial scales using a
2D hydraulic model and a 1D population model, Ecological Modeling, 265, 207-220, 2013.
Description: Here, we present a hybrid modelling approach to simulate the spatial dynamics of macroinvertebrates in a section of the Merced River in central California, re-engineered to improve the viability of Chinook salmon. Our efforts focused on quantifying the influence of the hydrodynamic environment on invertebrate drift dispersal, which is a key input to salmon bioenergetics models.
Swarming
A. Kolpas, M. Busch, H. Li, I. D. Couzin, L. Petzold, and J. Moehlis, How the Spatial Position of Individuals Affects their Influence on Swarms: A Numerical Comparison of Two Popular Swarm Dynamics Models, PLOS ONE, 8, No. 3, e58525, 2013.
Description: Schools of fish and flocks of birds are examples of self-organized animal groups that arise through social interactions among individuals. We numerically study two individual-based models, which recent empirical studies have suggested to explain self-organized group animal behavior: (i) a zone-based model where the group communication topology is determined by finite interacting zones of repulsion, attraction, and orientation among individuals; and (ii) a model where the communication topology is described by Delaunay triangulation, which is defined by each individual’s Voronoi neighbors. The models include a tunable parameter that controls an individual’s relative weighting of attraction and alignment. We perform computational experiments to investigate how effectively simulated groups transfer information in the form of velocity when an individual is perturbed.
Swimming capabilities
A. Kolpas, F. E. Fish, A. Meade, M. A. Dudas, and K. W. Moored. Mathematical analysis of
three-dimensional open water maneuverability by mantas (Manta birostris), presented by A. Kolpas and A. Meade at SIAM Computational Science and Engineering
Conference, Boston, MA, February, 2013.
Description: This research is the result of a new collaboration with Dr. Frank Fish (biology, WCU) and Andrew Crossett (statistics, WCU). The basis for the research is the development of sophisticated algorithms to better quantify turning maneuvers and swimming capabilities of animals including rays, beavers, and dogs through three-dimensional space.
Dr. Chuan Li
(Talk) Improvements on a matched interface and boundary (MIB) method for solving parabolic interface problems, SIAM CSS 2016, University of Arkansas at Little Rock, Sep 30 – Oct 2, 2016
(Talk) High-performance parallel computing algorithms for calculating electrostatic potentials and energies for large biological macromolecules and their applications in DelPhi, The Tenth International Conference on Scientific Computing and Applications (ICSCA2016), Toronto, Ontario, June 6-10, 2016
(Manuscript) Chuan Li and Shan Zhao, “A matched Peaceman-Rachford ADI method for solving parabolic interface problems”, Journal of Applied Mathematics and Computation, submitted on May 11th 2016.
Modeling Infectiology and Optimal Control of Malaria Epidemic
Collaborator: Prof. Baoling Ma, Department of Mathematics, Millersville University
Description: Malaria infection has been posing a major health threat for hundreds of years in
human history, yet no sophisticated mathematical models exist to study its dynamics
within an infected host due to complex interactions between the host immune response
and the parasite. In this project, we propose a new system of structured partial differential
equations, accounting for the dependence of red blood cell infectivity on its maturation
level and the time delay for the developmental period of the parasite to investigate
the population dynamics of Plasmodium falciparum and its interaction with red blood
cells and cells of the immune system. High-resolution finite difference schemes will
be developed to solve the system and deliver accurate numerical simulations. The newly
developed model will be applied to study the interplay between the host immune response
and the parasite dynamics and investigate crucial experimental parameters for reliable
prediction of treatment strategies.
Constructing Minimal Molecular Surface via MPI
Collaborator: Prof. Shan Zhao, Department of Mathematics, University of Alabama
Description: Modeling biomolecular surface is a challenging task due to molecules complicated
structures. The resulting surface has a great impact on the accuracy of all biomolecular
structure and interactions related studies and analysis. Conventional molecular surface
(MS) models are lack of physical justification and usually admit geometrical singularities.
In the contrast, a recently derived minimal molecular surface (MMS) model delivers
minimized surface area and surface free energy, which occurs naturally when a less
polar macromolecule is immersed in a polar aquatic environment. A fast alternating
direction implicit (ADI) algorithm has been developed to solve the governing differential
equation for MMS generation. However, the present ADI method implemented as a sequential
code is still prohibitively expensive in solving ultra large protein systems, such
as large protein complexes, that may have over one million atoms. In this project,
we propose to introduce new parallel computing techniques to significantly improve
the performance of the ADI solver. A MPI-parallelized software package, which is able
to effectively model molecular surface for extremely large macromolecules and complexes,
will be developed. Upon completion, the MMS generator will be released online as a
free software package for academic and research purposes. Funds are requested to disseminate
the research findings and showcase the software product to related research societies.
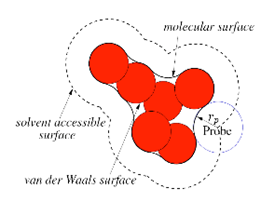
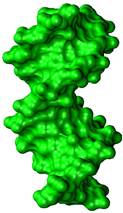
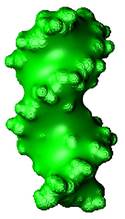
Figure 1. Left: The molecular surface (MS) is defined by rolling a probe sphere, which mimics the water molecule, around the Van der Waals (VdW) atoms of a protein; Middle: MS of a B-DNA; Right: Minimal molecular surface (MMS) of a B-DNA. The MMS minimizes the surface area while enclosing all VdW atoms and is free of shape singularities.
Development of a Matched Interface and Boundary (MIB) method for solving parabolic equations with complex interfaces
Collaborator: Prof. Shan Zhao, Department of Mathematics, University of Alabama
Description: This work aims to overcome difficulties of the previous matched Alternate Direction Implicit (ADI) method for solving parabolic equations with complex interfaces. In general parabolic interface problems, the discontinuities in a function and its flux across an interface are prescribed as spatially and temporally dependent jump conditions. Without addressing such conditions, the central difference spatial approximation is known to be inaccurate in the classical ADI schemes. This motivates the development of a matched ADI method in the literature, in which the central difference is locally corrected according to essentially one-dimensional (1D) jump conditions. Based on the Douglas ADI (D-ADI) in time, this matched D-ADI method is unconditionally stable and restores the second order of accuracy in space for geometries with simple interfaces. In order to make the developed ADI method works for geometries with complex interfaces, a formal temporal discretization is formulated which avoids extra perturbations of the original matched ADI framework. Second, the approximations to tangential derivatives are substantially improved in the tensor product decomposition of 2D or 3D jump conditions so that the essentially 1D jump conditions become more stable.
Development of Schemes for Parallel Computing of the Electrostatics in Biological Systems: Implementation in DelPhi
Collaborator: Prof. Emil Alexov, Department of Physics and Astronomy, Clemson University
Description: Nowadays, calculating the electrostatic potential and corresponding energies has become a standard computational approach for studying biomolecules and nano-objects immersed in water and salt phase. One most recognized math model in the area of molecular biology is the Poisson-Boltzmann Equation (PBE), for which no analytical solutions are available for irregular-shaped molecules and proteins, and the distribution of the potential can only be found numerically. However, no existing sequential PBE solver is ready to be utilized to solve PBE for large macromolecules and macromolecular complexes due to high computational time and memory requirements. In order to make the calculations feasible for large macromolecules and complexes, a set of computing schemes was introduced to parallelize the processes of molecular surface construction, numerical Successive Over Relaxation (SOR) iteration, and energy calculations. The parallelization schemes are implemented in the popular software DelPhi (http://compbio.clemson.edu/delphi) and results in speedup of several folds. As a demonstration of the efficiency and capability of this methodology, the electrostatic potential, and electric field distributions are calculated for several large macromolecules and complexes to illustrate their complex topology, which cannot be obtained by modeling the super-complex components alone.
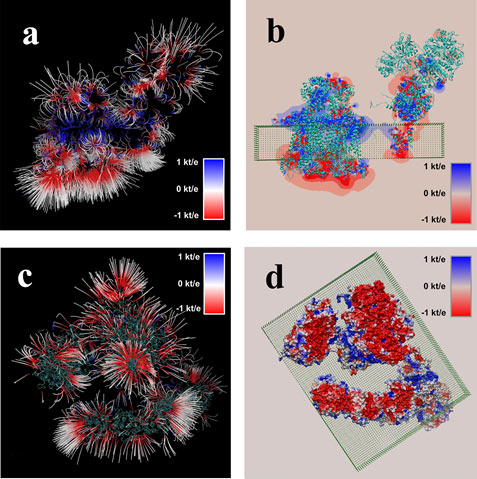
Resulting electrostatic field and potential maps of the bovine mitochondrial supercomplex. Membrane is shown as a slab made of pseudo atoms. a) Electrostatic field distribution in case of side-view; b) Potential distribution in a plane at the center of the supercomplex, side-view. The protein moiety is shown as well; c) Electrostatic field distribution in case of membrane-view; and d) Electrostatic potential mapped onto molecular surface of the supercomplex, membrane-view. The protein moiety is shown as well.
Dr. Mark McKibben
- Mahmudov, N.I. & McKibben, M.A., On approximately controllable systems, Applied and Computational Mathematics, volume 15, number 3, 247 – 264, October 2016.
- Lakhel, E. & McKibben, M.A., Controllability of neutral stochastic integro-differential evolution equations driven
by a fractional Brownian motion, to appear in Afrika Matematika.
- McKibben, M.A., General existence results for abstract McKean-Vlasov stochastic equations with variable
delay, Far East Journal of Mathematical Sciences, volume 99, number 9, 1335 – 1370, May 2016.
- Abstract Fractional Stochastic Evolution Equations with Applications to Nonlinear Beam Dynamics and Stochastic Wave Equations, 11th American Institute of Mathematical Sciences Conference on Dynamical Systems, Differential Equations and Applications, Symposium on Infinite Dimensional Stochastic Systems and Applications, Orlando, FL, July 2016 – invited symposium talk.
- Holey Rocks, Indecisive Fluids, Vanishing Beaches & Fiery Neurons: The Unifying Nature of Implicit Evolution Equations, Villanova University, August 2016 - invited colloquium talk.
- M. A. McKibben and M. Webster (Eds.), “Brownian Motion: Elements, Dynamics, and Applications,” Nova Science Publishers, November 2015.
Description: This volume focuses on recent research directions in the area stochastic analysis with the goal being to illustrate the path Brownian motion has taken over the past century. Together, Dr. Micah Webster and I compiled a volume comprised of fifteen different chapters illustrating distinct facets of work that involve Brownian Motion, including stochastic differential equations, controllability and optimal controllability, mathematical physics, robotics, and literature.
I co-wrote the following two chapters of this volume as well.
- E. Lakhel and M. A. McKibben, “Controllability of Impulsive Neutral Stochastic Functional
Integro-Differential Equations Driven by Fractional Brownian Motion,” Chapter 8 in:
Brownian Motion: Elements, Dynamics, and Applications, Editors: M.A. McKibben and M. Webster, Nova Science Publishers, November 2015.
- M. A. McKibben and M. Webster, “Abstract Second-Order Stochastic Evolution Equations
in a Hilbert Space Driven by Fractional Brownian Motion,” Chapter 15 in :Brownian Motion: Elements, Dynamics, and Applications, Editors: M.A. McKibben and M. Webster, Nova Science Publishers, November 2015.
- N. Mahmudov & M.A. McKibben, On the approximate controllability of fractional evolution equations with generalized Riemann-Liouville fractional derivative, in Special Issue “Recent Developments on Fixed Point Theory in Function Spaces and Applications to Control and Optimization Problems,” Journal of Function Spaces, April 2015, 9 pages.
Description: Controllability results for equations with generalized Riemann-Liouville fractional derivative were established in this paper. This class of equation arises in the study of various nonlinear diffusion processes and viscoelasticity.
- M.A. McKibben & M. Webster, Abstract Stochastic Integro-differential Delay Equations Driven by Fractional Brownian Motion, Far East Journal of Mathematical Sciences, volume 96, number 6, March 2015, 757 - 800.
Description: Existence results for abstract stochastic integro-differential equations with finite delay driven by fractional Brownian motion were established in this paper. Numerical simulations were also included to illustrate the applicability of the abstract theory to certain partial differential equations arising in diffusion and thermodynamics.
- M.A. McKibben, Measure-Dependent Stochastic Nonlinear Beam Equations Driven by Fractional Brownian Motion, International Journal of Stochastic Analysis, vol. 2013, Article ID 868301, 16 pages, 2013. doi:10.1155/2013/868301.
Description: This paper studies the well-posedness of a stochastic model for the dynamic buckling of a beam subject to various types of environmental noise.
- M.A. McKibben & M. Webster, Abstract Functional Stochastic Evolution Equations Driven by Fractional Brownian Motion, Abstract and Applied Analysis, vol. 2014, Article ID 516853, 14 pages, doi:10.1155/2014/516853.
Description: This paper establishes theoretical results that can be applied to mathematical models involving stochastic partial differential equations arising in various areas of study, including nonlinear diffusion, fluid flow through fissured rocks, and wave propagation.
