Applied Math Seminar
Under the dual guidance of Dr. Chuan Li and Dr. Andreas Aristotelous, our group has launched a seminar in which current topics in Applied Mathematics and Computational Science in general will be discussed. Seminars are scheduled in conjunction with the department’s colloquium series.
Many computational biophysics models can be categorized as the parabolic interface problems, in which the propagation of a physical quantity (heat, potential, etc.) across a material interface is modeled by a parabolic Partial Differential Equation (PDE). The standard numerical methods for solving PDE models often perform poorly on the parabolic interface problems due to the fact that the solutions may be non-smooth, or even discontinuous, across the arbitrarily shaped interface of two media. In this talk, I will present a previously developed method, called the Ghost Fluid Method (GFM), for solving elliptic interface problems, and demonstrate a recent development to improve its performance and combine it with appropriate implicit time evolution methods for solving 2D and 3D parabolic interface problems with various complex interfaces. This work is collaborated with Dr. Shan Zhao from the University of Alabama.
Speaker: Dr. Chuan Li (WCU Math)
Thursday April 26th, 2018 UNA 158, 3:25 - 4:25 PM
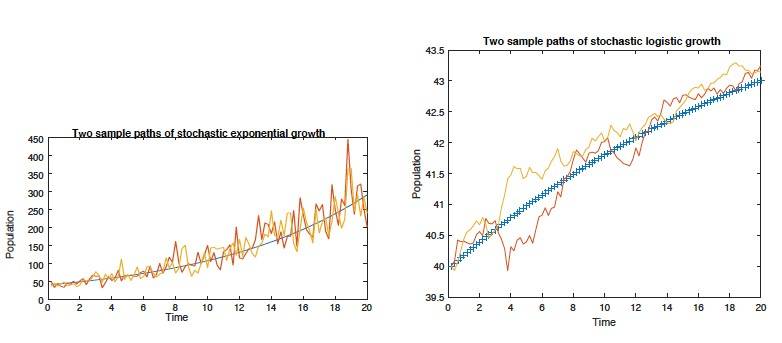
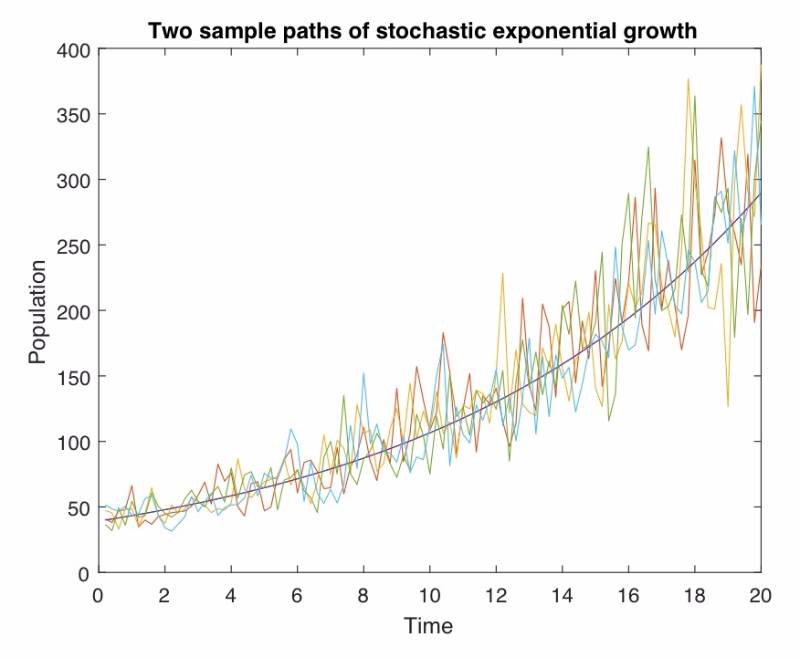
Modeling is one application that most people associate to mathematics, something that the non-mathematician can see, use and appreciate. Most models are inherently off, usually that either the model is not quite right and/or the parameters are good guesses. Modeling with stochastic differential equations models the phenomenon and the `noise'. This noise can be used in a number of ways, one being the natural error in the usual models. We will introduce how to model populations using stochastic differential equations with analytic and numerical examples (an emphasis on the numerical models). We only assume that the student knows the main ideas from calculus and a little statistics (mainly the standard normal random variable) which we will review.
Dr. Peter Zimmer (WCU Math)
Date: Wednesday April 4th, 2018, UNA 155, 3:15 - 4:15 PM
Abstract: Some students, having seen the seminar last fall, asked for more details on the subject, thus we will be REPEATING the same seminar from November 7, 2017 (last fall), with some more examples of computing stochastic ‘derivatives’ and stochastic integrals. Below is a description of last fall’s seminar. In two weeks, March 21, we will have a continuation of this seminar (model various growths processes like stock prices and predator-models).
We will introduce stochastic differential equations, which are ordinary differential equations with a random component. We could use this random component in many manners, one in particular is modeling an error term. So you could think of SDE (stochastic differential equations) as an ode (ordinary differential equation) with a built in error term. This lecture will develop what is called stochastic calculus which will be used to solve some SDEs. We will continue this discussion next spring to include numerical solutions to SDEs with many examples.

Dr. Peter Zimmer (WCU Math)
Date: February 21st, 2018, UNA 155, 3:15 - 4:15 PM
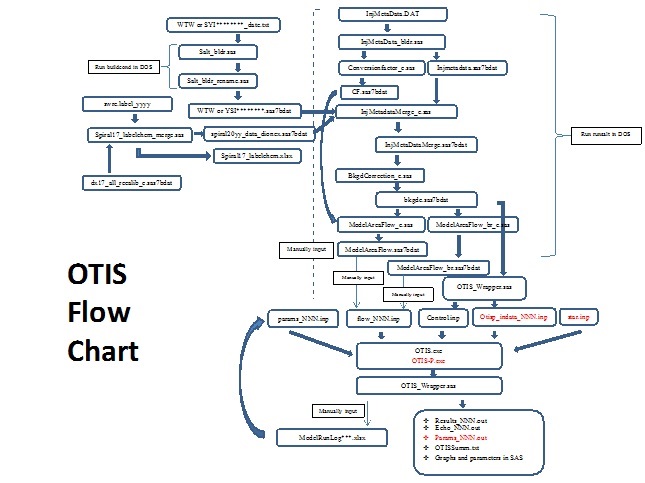
Solute transport in streams and rivers is governed by several differential equations for the hydrologic and geochemical processes. Knowledge of solute fate and transport is needed to aid estimating nutrient uptake in streams, estimating particulate transport, and assessing the fate of contaminants that are released into surface waters. OTIS is a mathematical simulation model used in conjunction with field-scale data to quantify hydrologic processes (advection, dispersion, and transient storage) affecting solute transport and certain chemical reactions (sorption and first-order decay). With given quantities, such as, the mass of the solute and the distance of the reach in the stream, OTIS determines the solute concentrations that result from hydrologic transport and chemical transformation. In this presentation, I demonstrate the application of OTIS with the field data from White Clay Creek and the experimental flumes for my intern experience and current part-time job at Stroud Water Research Center. Our experimental work on the streams and the data analysis using OTIS will help scientists to better understand the solute transport in the local streams and help estimating contamination in the local streams if it happens in the future.
Xiaojuan (Cathy) Yu (WCU Math)
Date: Wednesday Jan 31st, 2018, UNA 155, 3:10 - 4:10 PM
Mentors: Allison Kolpas, Dr. Chuan Li
Cryptography could be regarded as “applied number theory”, and modern cryptography is also heavily reliant on computers, so modern cryptography is also highly computational. In this talk the mathematics behind some modern public key cryptosystems are examined (in a public key cryptosystem, the enciphering key is public knowledge, and anyone can encipher and send a message, but only someone with deciphering key can decipher an enciphered message).
This talk will require little mathematics beyond multiplication of integers, and the concept of a remainder when one integer is divided by another.

James Mc Laughlin (WCU Math)
Date: 12/06/2017, Time: 3:15-4:15pm, Room: UNA 155
The notion of negative refraction goes back to the work of V. Veselago in the late 1960’s, in which he proposed that light can be bent in such a way that when light strikes a surface, the refracted ray makes a negative angle with the normal. Materials possessing such property do not exist naturally, but have been constructed in the laboratory in the early 2000’s. The research on the behavior of these materials, called metamaterials, has been extremely active in recent years, especially for applications to invisibility cloaking and the development of a “superlens", which can in principle image objects at the smallest scales. In this talk, I will discuss certain refraction problems in the setting of metamaterials. In particular, I will show how to obtain weak solutions (defined analogously to Brenier solutions for the Monge-Ampère equation) to these problems. For one variant of these problems, as in the case of positive refractive indices, a fully nonlinear PDE of Monge-Ampère type arises. Along the way, I will show that surfaces possessing a certain uniform refraction property, in the setting of metamaterials, are in general neither convex nor concave, which greatly contrasts with the case of positive refractive indices. This last result is joint work with Cristian Gutiérrez (Temple).

Eric Stachura (Department of Mathematics, Haverford College)
Date: 11/08/2017, Time: 3:15-4:15pm, Room: UNA 155
We will introduce stochastic differential equations, which are ordinary differential equations with a random component. We could use this random component in many manners, one in particular is modeling an error term. So you could think of sde (stochastic differential equations) as an ode (ordinary differential equation) with a built in error term. This lecture will develop what is called stochastic calculus which will be used to solve some sdes. We will continue this discussion next spring to include numerical solutions to sdes with many examples.
Peter Zimmer (WCU Math)
Date: 11/01/2017, Time: 3:15-4:15pm, Room: UNA 155
Talk Abstract
Fitness is environment-specific, and many organisms have evolved the ability to alter resource allocation based on perceived environmental cues (e.g., food/mate availability, predation risk). We are developing an optimization model that examines relative resource allocation into growth, reproduction, and defensive morphology under varying conditions. Specifically, we are investigating how reproductive investment in terms of rate and amount changes as a function of predation risk. The survival function utilizes a modified Gompertz-Makeham law for mortality. The fecundity function is the product of the reproductive schedule and output. The reproductive schedule utilizes a gamma distribution and the output is modeled exponentially. Optimizing the fitness model yields the optimal resource allocation and resulting reproductive schedule. This allows us to understand the effects of phenotypic plasticity in life-history traits on the evolution of a post-reproductive period. As predation risk increases, more resources are allocated towards defenses. However, once predation risk is sufficiently high, it becomes more beneficial for the individuals to allocate all their resource towards reproduction.

Mr. D’Alessandro, Lane A. (WCU Math)
Date: 04/12/2017, Time: 3:15-4:15 pm, Room: UNA 158
Mentor: Dr. Allison Kolpas
Talk Abstract
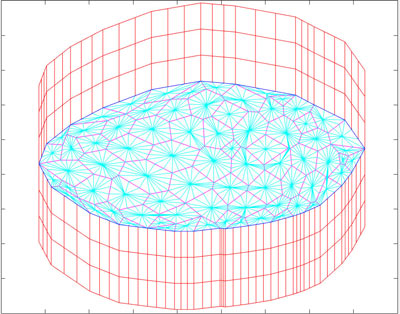
A model is being developed that simulates the dorsal closure process, a stage of drosophila embryogenesis. The apical side of the amnioserosa (a cell monolayer- wound like region on the surface of the embryo) is being represented through polygonal two dimensional representations of cells, with forces acting on their edges and nodes. Those forces are being regulated by the action of actin and myosin. The model is granular enough so various subregions can be studied to the level of the individual cell. Various equations are being tested, describing the evolution of forces generated by the action of the actomyosin network, which itself might be biochemically driven. Eventually, the model may be used to understand mechanisms of dorsal closure that are not easily analyzed in the lab or produce simulation results that might drive new experiments.
For further information about the Computational Sciences and Applied Mathematics Seminar, e-mail aaristotelous@wcupa.edu or cli@wcupa.edu
Mr. Ben Plumridge(WCU Math)
Date: 04/12/2017, Time: 3:15-4:15 pm, Room: UNA 158
Mentor: Dr. Andreas Aristotelous
Talk Abstract
Microbes form a large and central part of the global ecosystem. As a consequence of their short reproductive time and their proficiency at exchange of genetic material, it seems plausible that microbes in communities operate at high efficiency (in terms of free energy and nutrient usage) in many contexts. One obvious issue of interest would be the description of species within a microbial community and its dependence on the local environment. Description of niche structure of organisms and how that structure impacts competitiveness has long been a topic of interest among ecologists. Here, in the context of Yellowstone National Park microbial mat, we discuss influence of temporal environment on microbial community species structure. The possibilities of competitive exclusion and clocking behavior are discussed.

Biographical Note:
Professor Isaac Klapper is an expert in fluid dynamics and the mathematical modeling of the various aspects of biofilm formation, evolution and its interactions with its environment. He is the author of numerous publications and the receiver of several grant awards. He received his A.B. in Mathematics from Harvard University in 1986 and his PhD in Applied Mathematics from the Courant Institute, New York University (NYU) in 1991. He was an NSF postdoctoral fellow at the University of Arizona and a visiting assistant professor at UCLA in the Departments of Applied Mathematics. He served as a tenure-track and tenured faculty and rose to the rank of Full Professor at Montana State University where he was also affiliated with the Center of Biofilm Engineering (CBE) at Montana State. In 2012 he moved to Temple University with the appointment of Full Professor, Department of Mathematics with secondary appointment in the Department of Biology.
For further information about the Computational Sciences and Applied Mathematics Seminar, e-mail aaristotelous@wcupa.edu or cli@wcupa.edu
Professor: Isaac Klapper
Department of Mathematics, Temple University
Date: 04/05/2017, Time: 3-4pm, Room: UNA 158
Abstract:
In ecological studies, identifying the number of species present in an ecosystem, also known as identifying the species richness, is key to measuring biodiversity and ecological stability. In order to analyze the species richness of a system, we performed a process known as rarefaction. Through rarefaction, we attempted to identify the number of samples needed to accurately represent a system.
We examined different methods of performing rarefaction, including the combinatorics method and the bootstrap method, and compared them. Both of these methods allowed us to construct a rarefaction curve that plots the number of species as a function of the number of samples taken. Using these rarefaction curves, we then extended the model by examining initial costs and coverages of the samples. These examinations served to identify the number of samples needed to represent the ecosystem. Once we identified the number of samples needed, we compared the results of different months and locations.
As a possible cause of any present differences between months and locations, we examined the number of degree days that occurred over each month. Degree days did not appear to cause any differences between locations.
Lane D’Alessandro and Maggie Celentano
Date: 03/22/2017, Time: 3:15-4:15pm, Room: UNA 158
Mentor: Dr. Allison Kolpas
Abstract:
We are studying which abiotic parameters best explain the presence or absence of brown trout in White Clay Creek and will subsequently use those parameters to develop a Habitat Suitability Index (HSI). The goal of finding an HSI for different habitats is to help researchers improve decision making and increase understanding of species-habitat relationships. Using the dataset provided by Stroud Water Research Center, we are analyzing the correlation or lack thereof between environmental factors and the quantity of brown trout present in that environment. Using fuzzy logic, we are developing a model to determine an HSI, which is a numerical index that represents the capacity of a given habitat to support a selected species.
For further information about the Computational Sciences and Applied Mathematics Seminar, e-mail aaristotelous@wcupa.edu or cli@wcupa.edu
Ben Plumridge and Cathy Yu
Date: 03/22/2017, Time: 3:15-4:15pm, Room: UNA 158
Mentor: Dr. Allison Kolpas
Abstract
The sperm whale is the largest toothed whale. It is currently on the list of vulnerable species by theInternational Union for the Conservation of Nature and Natural Resources (IUCN). Even though a lot of research has been dedicated to sperm whales, very little is known about their population dynamics. In this talk I will first go over the brief results of our study to investigate the demographic characteristics of the endangered sperm whale population. Our results indicate that these survivorship rates are very delicate, and a slight decrease could result in a declining population, leading to extinction.
The Deepwater Horizon (DWH) oil rig exploded in April of 2010. This environmental disaster has encouraged substantial research efforts to better understand how such disasters affect the resilience of the Gulf of Mexico (GoM) ecosystem. In this talk I will demonstrate how mathematical models can be applied to understand the impacts of such disasters on the dynamics and persistence of marine mammal populations in the Northern GoM under certain assumptions. Matrix population models are developed to study the lethal and sub-lethal impacts. We investigate how reductions in the survival probabilities and in fecundity affect the sperm whale population. We then investigate the long term effect of such an environmental disaster on the population of sperm whales in the GoM. We also inspect the effects of demographic stochasticity on the recovery probabilities and the recovery time of the population.

For further information about the Computational Sciences and Applied Mathematics Seminar, e-mail aaristotelous@wcupa.edu or cli@wcupa.edu
Dr. Baoling Ma
Assistant Professor of Mathematics, Department of Mathematics, Millersville University
Date: 02/22/2017, Time: 3-4pm, Room: UNA 158
Abstract
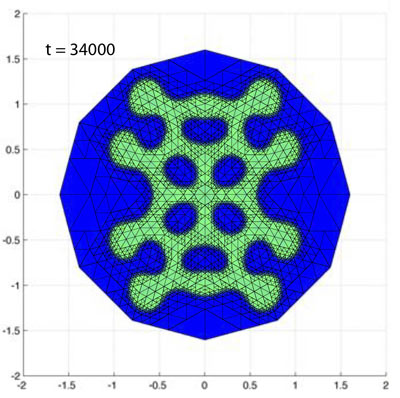
Partial Differential Equation Models based on Cahn-Hilliard type equations will be discussed. Those Models have applications in various fields from material science to biology. Discontinuous Galerkin Finite Element Methods for the solution of Cahn-Hilliard type equations will be presented. For the underline schemes: solvability, energy stability, convergence and error estimates will be established. Simulation results will be provided. Current and future directions will be discussed.
For further information about the Computational Sciences and Applied Mathematics Seminar, e-mail aaristotelous@wcupa.edu or cli@wcupa.edu
Dr. A. C. Aristotelous
Department of Mathematics, West Chester University
Date: 02/15/2017, Time: 3-4pm, Room: UNA 158
Abstract
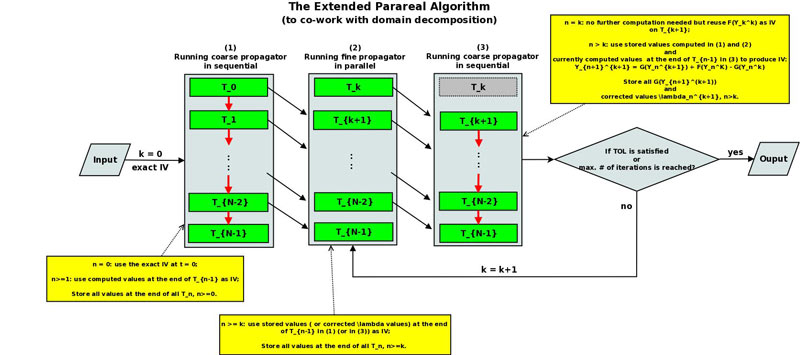
The Parareal Algorithm introduced by Jacques-Louis Lions, Yvon Maday, and Gabriel Turinici is an efficient method for achieving parallel computing in time direction for solving time-dependent partial differential equations. However, we have not seen in literature a method to effectively incorporate the spatial-parallelized schemes into the framework of the Parareal algorithm in order to obtain both temporal and spatial parallel computing. In this work, we present a work to extend the original Parareal algorithm to effectively embrace spatial-parallelized solvers to accomplish time-and-space parallel computing of the Cable equation on long cardiac tissues.
For further information e-mail mfisher@wcupa.edu or sgupta@wcupa.edu
Dr. Chuan Li
Department of Mathematics, West Chester University
Date: 11/10/2016, Time: 3:00-4:00pm UNA 125
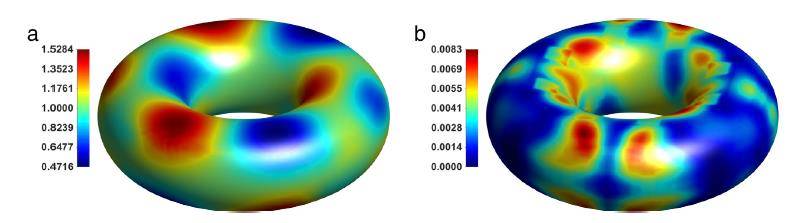
One common approach to study electrostatics in molecular biology is via numerically solving the Poisson-Boltzmann equation (PBE) and calculating the electrostatic potential and energies. However, all existing numerical methods for solving the PBE become intolerably slow when solving the PBE for large macromolecules and complexes consisting of hundreds of thousands of charged atoms due to high computational cost. Parallel computing is a cutting-edge technique which teams up multiple computing units and significantly speeds up the calculation. In this talk, I will present a set of parallel computing algorithms developed to solve the PBE. As a demonstration of efficiency and capability of these algorithms, computational results obtained by implementing these algorithms in the DelPhi software on live large macromolecules and complexes are given as well.
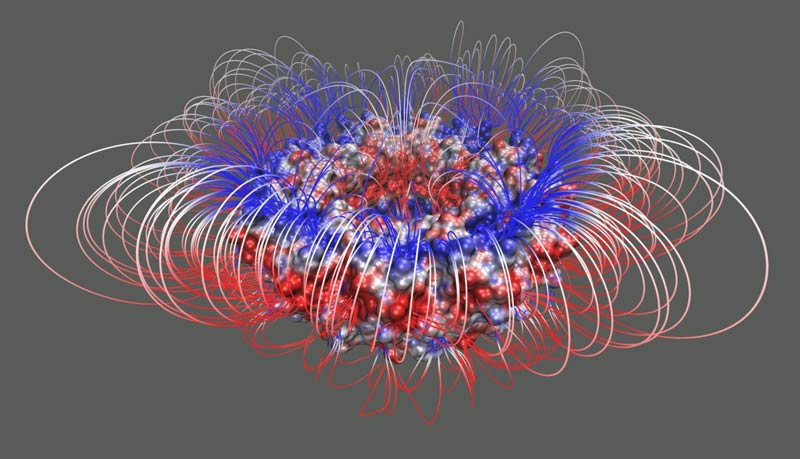
A computer generated electrostatic potential and field lines of the transcription attenuation protein after numerically solving the Poisson-Boltzmann equation.
Dr. Chuan Li
Department of Mathematics, West Chester University
Date: 10/26/2016, Time: 3:00-4:00pm UNA 125
All graduate students are encouraged to attend these seminars to gain exposure to various areas of applied mathematics.
