A Cellular Automaton

Update (12/10/2018): I was today informed that the first of these cellular automata is well-known and extensively studied. A google search for "B1357/S1357" , one of its official classifications, will bring up many hits. It is also known as "Replicator", and was discovered by Edward Fredkin.
This cellular automaton (CA) was found by me while preparing some material for my MAT 413 Computer Algebra class (essentially, it is a class about using a computer algebra system like Mathematica to assist in mathematical investigations).
I am not an expert on cellular autmata, so I am unaware if this is new, or has already been found (possibly many times over), and has been studied before. I would be grateful if anyone could direct me to either any sources about this particular cellular automaton, or could direct to someone who is a specialist in the area of cellular automata. Please email me at
Jimmy Mc Laughlin.
The CA starts, as is often the case, with an infinite array of 1x1 cells centered at the points with integer coordinates in the xy plane, with the square at the origin initially being black, and all other squares initially being white (generation 1).
The rule of transition from each generation to the next is that a square turns/stays coloured black if an odd number of its 8 neighbours are coloured black, and turns/stays coloured white if an even number of its 8 neighbours are coloured black.
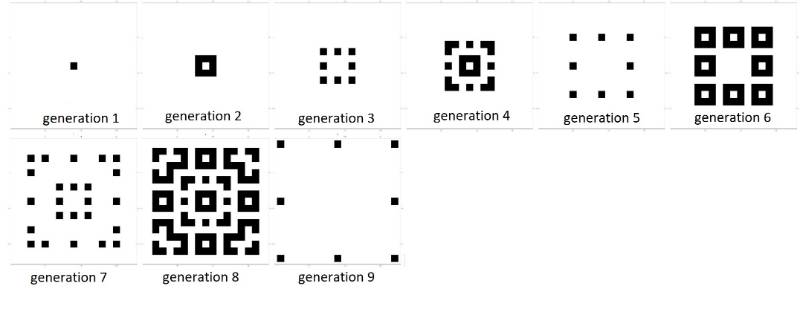
This CA appears to have some interesting properties:
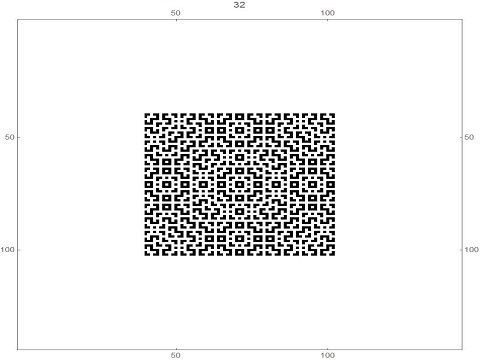
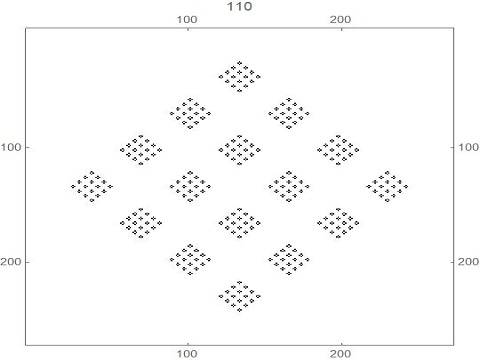
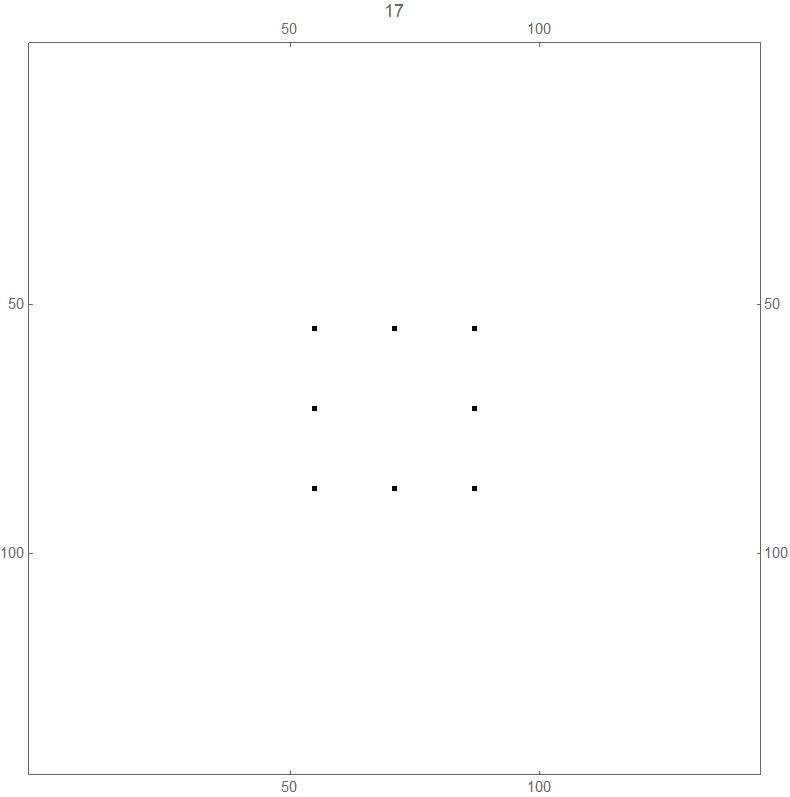
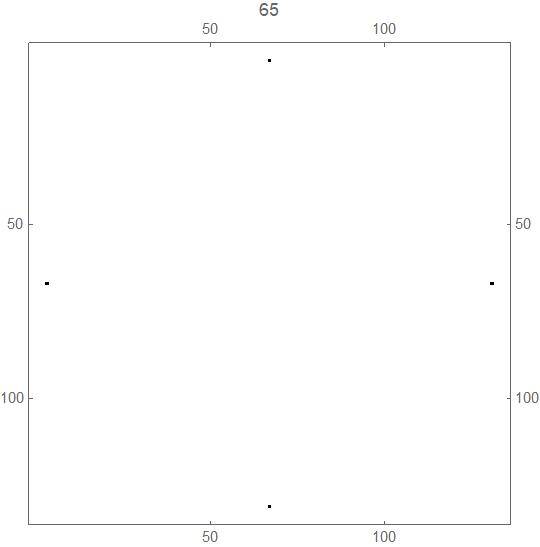
a) For each non-negative integer n, it appears that at generation 2n +1, there are just 8 black cells, at positions (+/- 2n, +/-2n), (+/- 2n,0) and (0,+/-2n) - see the pictures above for generations 3, 5 and 9, and below for generations 17, 33, 65 and 129.
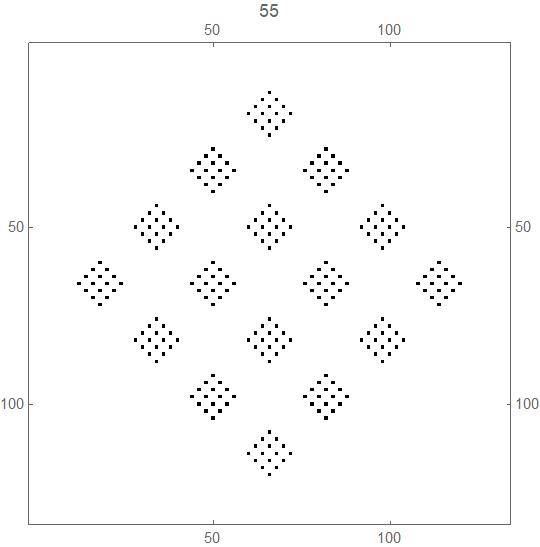
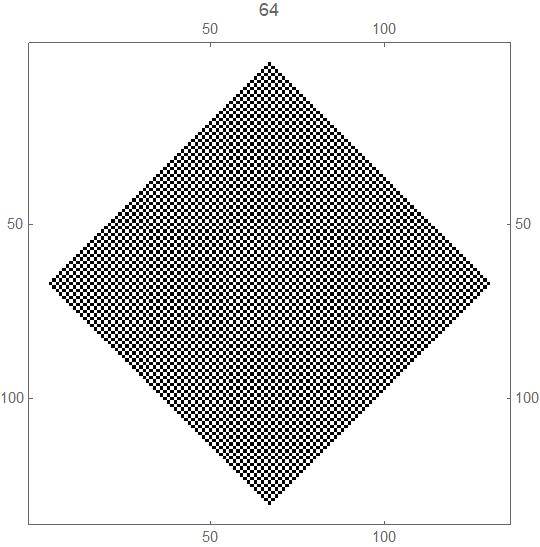
b) For each positive integer n, it appears that, at generation 2n , that both black squares and white squares are "dense" inside the box defined by the 8 points in part a), in the sense that each black square has at least one white square as a neighbour, and vice versa - likewise, see the pictures below for the transition from these generations to the ones following (described at a) above).
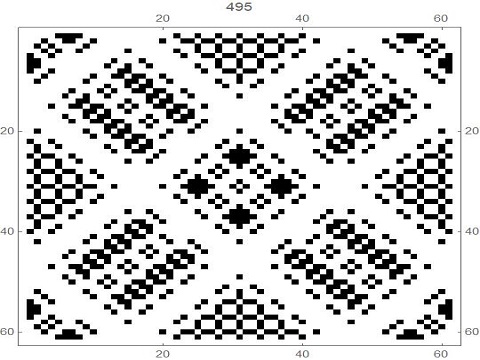
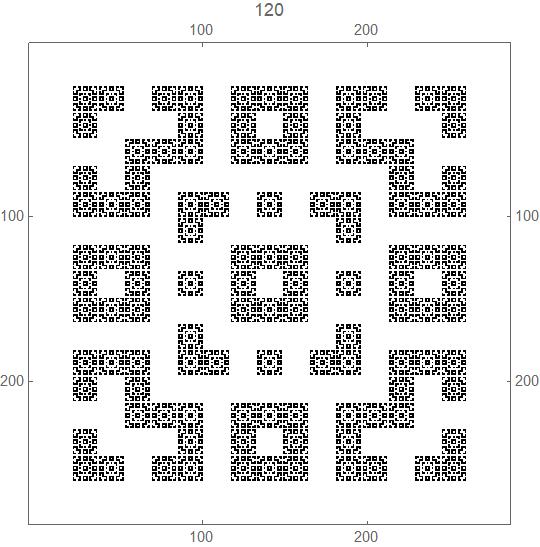
c) As the CA runs through the generations, it appears to exhibit fractal behavior. See below for example, where the pattern at generation 120 looks like the pattern at generation 8, while this same pattern may also be found within the 15x15 squares at generation 120 that correspond to the 1x1 black squares at generation 8.

The following video shows the cellular automaton running for 136 geerations.
The next video shows the cellular automaton running for 71 generations, and allows for a more detailed view of the pattern of black and white cells in these early generations.
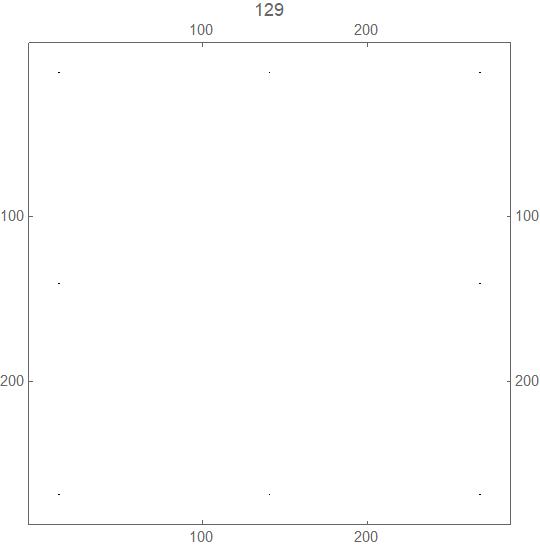
The transition from generation 128 (white and black squares both "dense" in the sense defined above) to generation 129 (just 8 black squares):

The transition from generation 64 (white and black squares both "dense" in the sense defined above) to generation 65 (just 8 black squares):


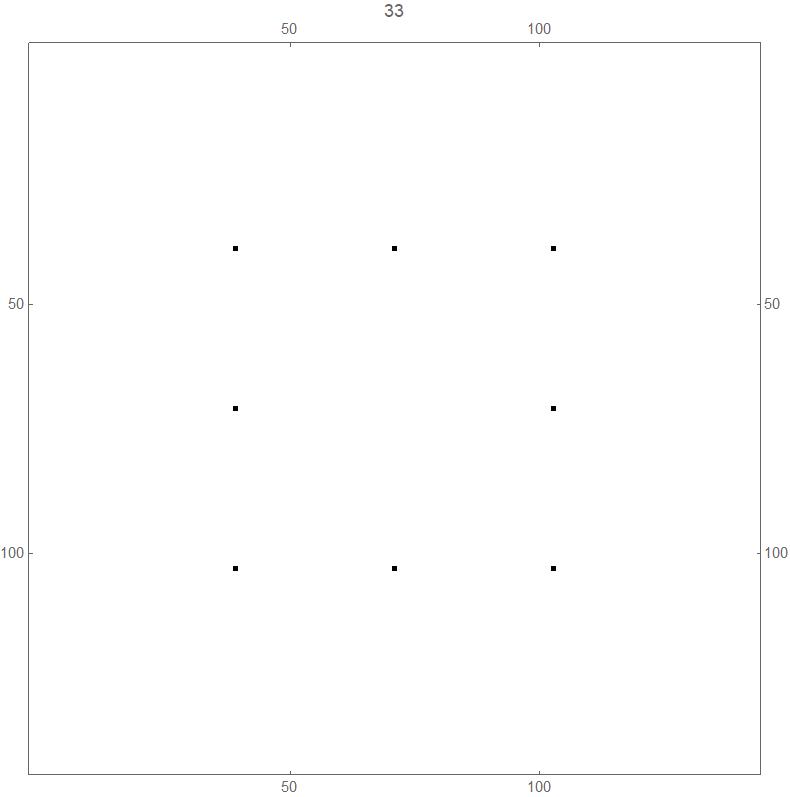
The transition from generation 32 (white and black squares both "dense" in the sense defined above) to generation 33 (just 8 black squares):

The transition from generation 16 (white and black squares both "dense" in the sense defined above) to generation 17 (just 8 black squares):

What if this cellular automaton is run on a 2k+1 x 2k+1 torus (alternatively, on a 2k+1 x 2k+1 array of squares, where the top and bottom edges are joined up, as are the right and left edges)?
The fact that the number of possible arrangement of black and white squares in a square array of side n is 2(n^2) means that the sequence of patterns must eventually start to cycle.
Experimental evidence suggests that the first repeated generation is always generation 2, and that for a torus of "side" 2k+1 this repetition occurs at generation 2mk + 1 for some integer mk.
The first few values of
(2k+1, first generation that repeats the pattern of generation 2 for a torus of "side" 2k+1)
are:
(3,3), (5,5), (7,9), (9,9), (11,33), (13,65), (15,17), (17,17), (19, 513), (21,65) and (23,2049).
Observe that several, but not all, of these fall into the pattern (2k+1, 2k +1). These include (3,3), (5,5), (7,9), (11,33), (13, 65), (19, 513) and (23, 2049).
The patterns are a little mesmerizing to watch. Here is the first 1031 generations of this cellular automaton running on a torus of side 61. At the exhibited rate, it should return to the pattern of generation 2 in about 36 days, if it follows the pattern (2k+1, 2k +1) mentioned above.
Some open mathematical questions (if this is a studied object, and the answers to the following questions/problems are known, I would very much appreciate pointers towards any discussion online or in the literature - email
Jimmy Mc Laughlin) are the following.
For this cellular automaton running in the infinite plane do each of the following:
a) For each non-negative integer n, prove or disprove that at generation 2n +1, there are just 8 black cells, at positions (+/- 2n, +/-2n), (+/- 2n,0) and (0,+/-2n) - see the pictures above.
b) For each positive integer n, prove or disprove that, at generation 2n , both black squares and white squares are "dense" inside the box defined by the 8 points in part a), in the sense that each black square has at least one white square as a neighbour, and vice versa.
c) Classify/describe the fractal nature of the pattern of black/white cells in particular generations (which generations display fractal behavior, what is the nature of the behavior).
d) When this cellular automaton runs on a torus, prove or disprove that the first generation whose patter repeats is generation 2.
e) If d) is true and given a torus of side 2k+1 where k is an arbitrary positive integer, determine the number of the generation, as a function of k, in which the pattern of generation 2 first repeats.
Finally, here is a Mathematica notebook with some elementary code that I used to examine this cellular automaton.
A Second Cellular Automaton
There is a second, closely related, related cellular automaton with similar properties, and a similar rule.
This was also discovered (rediscovered?) by me while preparing some material for my MAT 413 Computer Algebra class.
The CA starts, as with the above example, with an infinite array of 1x1 cells centered at the points with integer coordinates in the xy plane, with the square at the origin initially being black, and all other squares initially being white (generation 1).
The rule of transition from each generation to the next is that a square turns/stays coloured black if an odd number of its 4 neighbours are coloured black, and turns/stays coloured white if an even number of its 4 neighbours are coloured black.
The difference in the rule for this cellular automaton compared with the one above is that here "neighbours" are defined to the cells immediately to the north, south, east and west, whereas in the cellular automaton above, "neighbours" also included the cells immediately to the NW, NE, SW and SE.
The first 35 generations, showing the rule of this cellular automaton at work:
The first 133 generations, giving a better idea how this cellular automaton behaves:
This cellular automaton appears to have some interesting properties, similar to that of the cellular automaton described above:
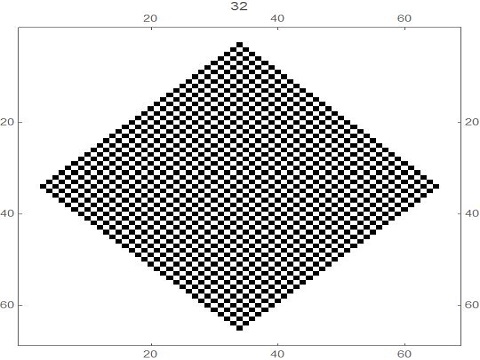
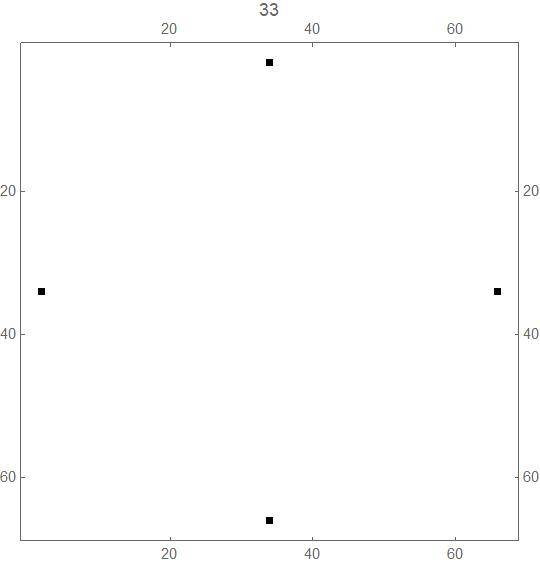
a) For each non-negative integer n, it appears that at generation 2n +1, there are just 4 black cells, at positions (+/- 2n,0) and (0,+/-2n) - see the pictures below.
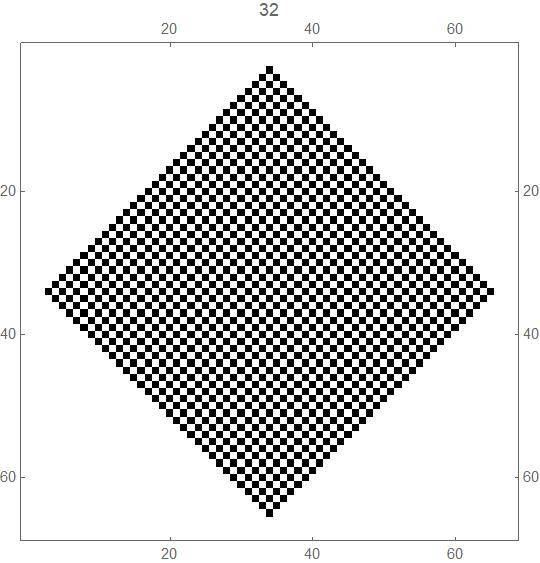
b) For each positive integer n, it appears that, at generation 2n , all squares inside the diamond defined by the 4 squares in a) are coloured alternately white and black, starting with white at the origin.
The transition from generation 64 (alternate white and black squares) to generation 65 (just 4 black squares):
The transition from generation 32 (alternate white and black squares) to generation 33 (just 4 black squares):
c) As the CA runs through the generations, it appears to exhibit fractal behavior,
although this time the fractal pattern is elementary, namely a diamond (see the picture
above, at the start of this section).
Strangely, or not so strangely, this cellular automaton exhibits behavior similar to the cellular automaton above when run on a torus.
Experimental evidence suggests once again that the first repeated generation is always generation 2, and that for a torus of "side" 2k+1 this repetition occurs at generation 2mk + 1 for some integer mk.
The first few values of
(2k+1, first generation that repeats the pattern of generation 2 for a torus of "side" 2k+1)
follow exactly the same pattern as for the cellular automaton above:
(3,3), (5,5), (7,9), (9,9), (11,33), (13,65), (15,17), (17,17), (19, 513), (21,65) and (23,2049).
Here is the first 800+ generations of this cellular automaton running on a torus of side 61. At the exhibited rate, it should return to the pattern of generation 2 in about 36 days, if it follows the pattern (2k+1, 2k +1) mentioned above.
Some open mathematical questions (if this is a studied object, and the answers to the following questions/problems are known, I would very much appreciate pointers towards any discussion online or in the literature - email Jimmy Mc Laughlin ) are the following.
Likewise, for this cellular automaton running in the infinite plane do each of the following (the proofs should be easier than for the cellular automaton above):
a) For each non-negative integer n, prove or disprove that at generation 2n +1, there are just 4 black cells, at positions (+/- 2n,0) and (0,+/-2n) - see the pictures above.
b) For each positive integer n, prove or disprove that, at generation 2n , all squares inside the diamond defined by the 4 squares in a) are coloured alternately white and black, starting with white at the origin..
c) Classify/describe the fractal nature of the pattern of black/white cells in particular generations (which generations display fractal behavior, what is the nature of the behavior).
When this cellular automaton runs on a torus,
d) prove or disprove that the first generation whose patter repeats is generation 2.
e) If d) is true and given a torus of side 2k+1 where k is an arbitrary positive integer, determine the number of the generation, as a function of k, in which the pattern of generation 2 first repeats.
Finally, here is another Mathematica notebook with some elementary code that I used to examine this second cellular automaton.