Research Interests
My research interests are focused on the development, theoretical analysis and implementation of efficient algorithms in view of their application to the simulation of problems of practical interest. My specialty is on the use of Discontinuous Galerkin Finite Element Methods (DG-FE) methods for the numerical solution of problems arising in biomedical and material sciences. Specifically, I am interested in the development and analysis of high order numerical schemes that accurately and efficiently resolve the solution to non linear equations like Cahn-Hilliard type equations, arising in models describing biological growth e.g. cancerous tumors and phase separation. Adaptive mesh refinement, (theoretical) error analysis and energy stability via convex splitting are also being addressed in my work. For the solution of the resulting algebraic (nonlinear) systems efficient solvers based on multigrid are designed.
The development of hybrid discrete cellular automata systems (HD-CA) by coupling linear and non-linear reaction diffusion partial differential equations with discrete (stochastic) cellular automata systems is also a part of my work. I utilize hybrid discrete systems to derive constitutive relationships and study phenomena in tissue engineering, cancer modeling, and evolutionary game theory. Another aspect of my research is related to the study of the various mechanisms governing the dorsal closure in the drosophila embryo through the development of individual based mechanistic models. The dorsal closure morphogenesis closely resembles the wound healing process in animal and human tissue, thus its study is of great importance.
Current Research Projects
I am looking for motivated students with love for mathematics that are interested in doing research. Ask me for more details!!
- With Professor Stephanos Venakides Duke Mathematics: Working on numerical solution to the semiclassical limit focusing (nonlinear) Schrodinger equation for small Planck constant.
- With Professor Isaac Klapper Temple Mathematics: We are interested in determining how biofilm spatial heterogeneity affects flux of substrate. In particular, we suggest that denser biomass encourages increased substrate flux -- substrate levels are further reduced for increased biomaterial which increases substrate gradients which leads to increased flux. Thus a flux-driven heterogeneity instability might be expected for a system for which growth rate is an increasing function of substrate usage. We are currently working on determining the effects of Neutrophils on biofilm formation.
- With Professors Ohannes Karakashian and Steven Wise, UTk: Working on topics related
to my NSF grant.
Discontinuous Galerkin Finite Element methods for the numerical solution of various Cahn-Hilliard type equations
Work involves development, convergence analysis (error estimates) and implementation of numerical schemes in primitive variable and mixed formulations, utilizing adaptive mesh refinement and fast linear and nonlinear system solvers. - With Professor Stephanos Venakides Duke Mathematics and Professor Dan Kiehart's Biology lab group also at Duke: Dorsal closure is a part of the Drosophila embryogenesis.It constitutes a model for cell sheet morphogenesis during development and wound healing. For this reason the study of the various mechanisms governing dorsal closure is of great importance. Here we strive to devise a flexible computational platform employing individual based modeling techniques that will allow us to incorporate experimental data and give us the freedom to test different kinds of modeling equations describing mechanistic or biochemical effects on the various parts of the simulated Drosophila embryo.
Publications
Numerical Analysis
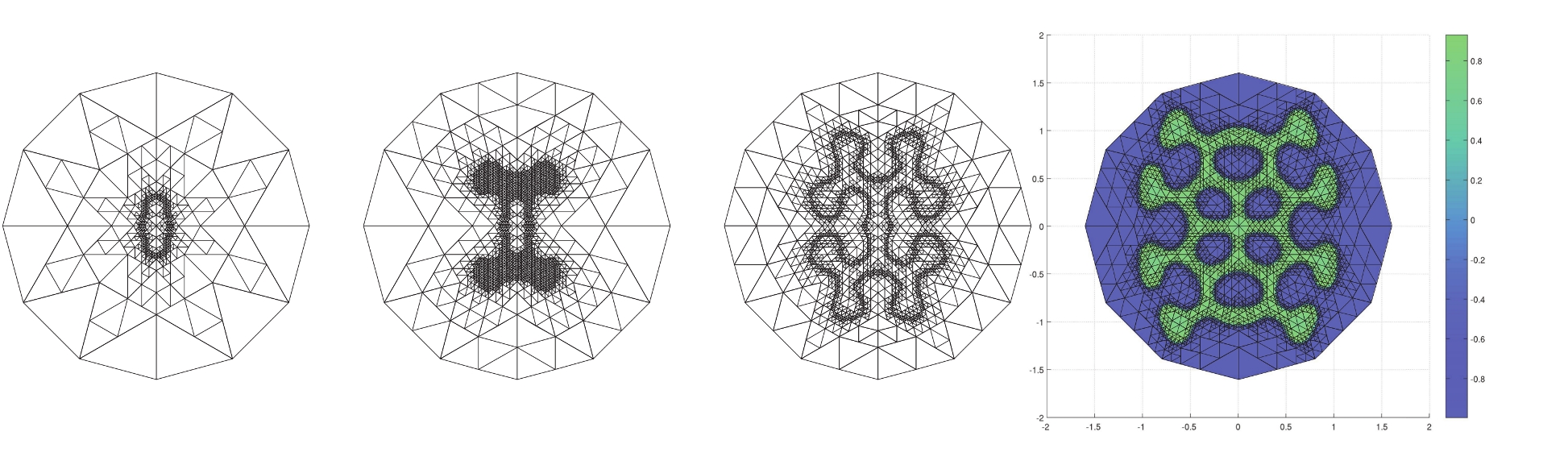
- Aristotelous, A. C., Karakashian, O. A. and Wise, S. M. (2015) Adaptive, Second-Order in Time, Primitive-Variable Discontinuous Galerkin Schemes for a Cahn-Hilliard Equation with a Mass Source. IMA J. Numer. Anal., 35-3, 1167--1198.
- Aristotelous, A. C., Karakashian, O. A. and Wise, S. M. (2013) A Mixed Discontinuous Galerkin, Convex Splitting Scheme for a Modified Cahn-Hilliard Equation and an Efficient Nonlinear Multigrid Solver. DCDS-B, 18-9, 2211--2238.
Hybrid Discrete Systems
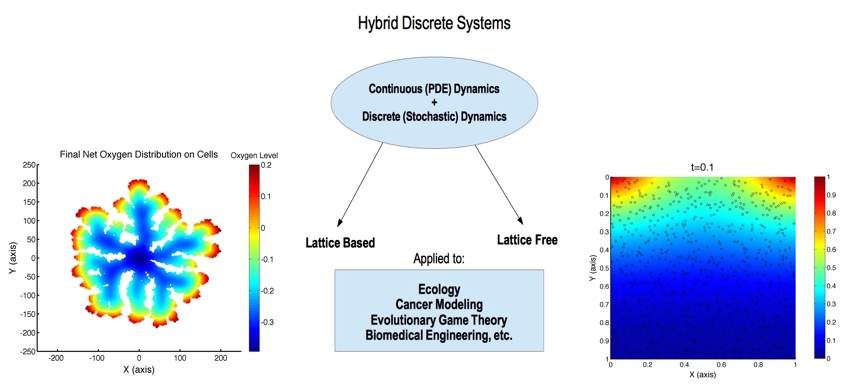
- Aristotelous, A. C., Grabovsky, Y. & Klapper, I. (2018) Heterogeneity Formation Within Biofilm Systems. European Journal of Applied Mathematics, 1-15.
- Aristotelous, A. C., Klapper, I., Grabovsky, Y., Pabst, B., Pitts, B. and Stewart, P. S. (2015) Diffusive Transport Through Host-Biofilm Systems. Phys. Rev. E , 92-2, 022703.
- Aristotelous, A. C. and Durrett, R. (2014) Fingering in Stochastic Growth Models. Experimental Mathematics, 23-4, 465--474.
- Aristotelous, A. C. and Haider, M. A. (2014) Evaluation of Diffusive Transport and Cellular Uptake of Nutrients in Tissue Engineered Constructs using a Hybrid Discrete Model. Processes: Special Issue ``Design of bioreactor systems for tissue engineering", 2-2, 333--344.
- Aristotelous, A. C. and Durrett, R. (2014) Chemical Evolutionary Games. Theoretical Population Biology, 93, 1--13.
- Aristotelous, A. C. and Haider, M. A. (2014) Use of Hybrid Discrete Cellular Models for Identification of Macroscopic Nutrient Loss in Reaction-Diffusion Models of Tissues. Int. J. Numer. Meth. Biomed. Engng., 30-8,767--780.
Computational Models
- A. C. Aristotelous & N. C. Papanicolaou (2017) A Numerical Study of Biofilm Growth in a Microgravity Environment. American Institute of Physics (AIP) Conference Proceedings, 1895, 120001.
Computational Fluid Dynamics
- Aristotelous, A. C. & Papanicolaou, N. C. (2016) A Discontinuous Galerkin Method for Unsteady Two-dimensional Convective Flows. American Institute of Physics (AIP) Conference Proceedings, 1773, 110002.
- Papanicolaou, N. C. and Aristotelous, A. C. (2015) High-Order Discontinuous Galerkin Methods for Coupled Thermoconvective Flows under Gravity Modulation. American Institute of Physics (AIP) Conference Proceedings 1684., 090010.
Review Papers
- Aristotelous, A. C., Crawford, J. M., Edwards, G. S., Kiehart, D. P. & Venakides, S. (2018) Mathematical models of dorsal closure. Progress in Biophysics and Molecular Biology, 137, 111--131
- Daniel P. Kiehart, Janice M. Crawford, Andreas C. Aristotelous, Stephanos Venakides & Glenn S. Edwards (2017) Cell Sheet Morphogenesis: Dorsal Closure in Drosophila Melanogaster as a Model System. Annual Review of Cellular and Developmental Biology, 33-1, 169--202.
PhD Dissertation
- Aristotelous, A. C. (2011) Adaptive Discontinuous Galerkin Finite Element Methods for a Diffuse Interface Model of Biological Growth. PhD Thesis, The University of Tennessee, U.S.A.
