Rep-tiles Revisited

Department of Mathematics, Anderson Hall 331a, West Chester University, West Chester, PA 19383

The goal of this note is to take a new look at some of the most amazing objects discovered in recreational mathematics. These objects, having the curious property of making larger copies of themselves, were introduced in 1962 by Solomon W. Golomb [2], and soon afterwards were popularized by Martin Gardner [3] in Scientific American. In Golomb's terminology a plane figure (or tile) is defined to be replicating of order k (or rep-k) if it can be dissected into k replicas, each congruent to the other and similar to the original one. If k=4, an equivalent definition is that four identical figures are to be assembled into a scale model, twice as long and twice as high. All triangles and parallelograms are rep-4 tiles. Besides these obvious examples, a great number of rep- tiles are known. We will review in this paper all known rep-4 convex polygons and a couple of rep-4 connected non-convex polygons. Our list originates in [2], where examples of rep-k tiles can be found for other values of k, as well as disconnected or fractal type examples. In what follows we are interested in the following question:

Question 1  Which polygonal rep-4 tiles are rep-k2 tiles for any k ≥ 4?

An equivalent formulation of the question is to find for which rep-4 tiles k2 identical figures can be assembled into a scale model, k times as high. If T is a given tile, we will call the scale model the k-th multiple of T, and for the rest of the paper will denote it by kT. Question 1 can be viewed as a particular case of the most general question:

Question 2 (Finite Tiling Problem)   Given a finite plane region T, and a finite set ∑ of tiles, find if T can be tiled by translations of tiles in ∑.

Let us only note here that methods do exist, coloring arguments among others, which can be used to prove non-existence of tilings. We refer the reader to [1],[4], and [5] for other techniques, some of them stronger then coloring arguments. An open question about non-existence of certain tilings related to reptiles will be mentioned during our exposition. The answer to Question 1 will be positive most of the time. The main technique used in the proof of our results is mathematical induction. Our proofs are not necessarily the shortest, or the most elegant, possible. We encourage the reader to try to find his own proofs before reading ours, and hope that this exercise will get him hooked in this fascinating field.

 

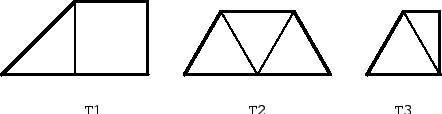
Figure 1: Diagram

 

As shown in Fig. 1, there are three trapezoids that are rep-4 tiles. We will denote them by T1, T2, T3. The first one consist of a square and a half, the second is made out of three equilateral triangles, and the third consists of an equilateral triangle and a half. We assume for the rest of the paper that the sides of the square and of the equilateral triangle are of length one.

Proposition 3   All three trapezoids T1, T2, T3, are rep-k2 tiles for any k ≥ 1.

Proof. For all three cases the proof is done by induction. We check first our hypothesis for k = 2, 3, and then show that rep-k2 implies rep-(k+3)2. Proof for T1. The cases k = 2, 3 are dealt with in Fig. 2. To show that rep-k2 implies rep-(k+3)2, we take a (k+3)T1 region and partially cover it by a kT1 region as shown in Fig. 3. The kT1 region can be covered by T1 tiles because of the induction hypothesis. The uncovered region can be decomposed in three parts: a rectangle (I) of dimensions (2k, 3), a rectangle (II) of dimensions (k, 3), and a region of type 3T1. The rectangles can be covered by rectangles of dimensions (3, 1), which in turn can be covered by two T1 tiles.

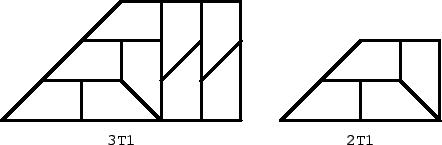
Figure 2

Figure 2:

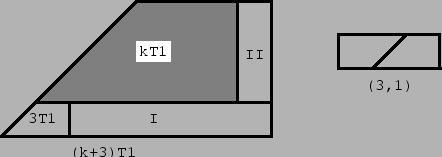
Figure 3

Figure 3:

Proof for T2. The cases k = 2, 3 are dealt with Fig. 4.

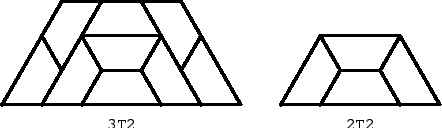
Figure 4

Figure 4:

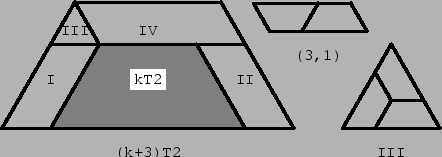
Figure 5

Figure 5:

To show that rep-k2 implies rep-(k+3)2, we take a (k+3)T2 region and partially cover it by a kT2 region as shown in Fig. 5. The kT2 region can be covered by T2 tiles because of the induction hypothesis. The region not covered by the kT2 region is decomposed in four parts: two parallelograms (I) and (II) of dimensions (k, 3), a parallelogram (IV) of dimensions (k+3, 3), and an equilateral triangle (III). All parallelograms can be covered by parallelograms of dimensions (3, 1), which consist of two T2 tiles, and the equilateral triangle can be covered by T2 tiles as in Fig. 5. Proof for T3. The cases k=2, 3 are dealt with in Fig. 6.

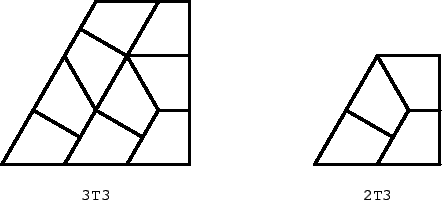
Figure 6

Figure 6:

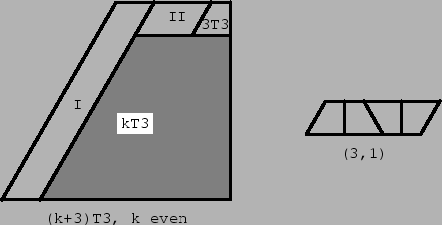
Figure 7

Figure 7:

Figure 8

Figure 8:

To show that rep-k2 implies rep-(k+3)2, we take a (k+3)T3 region and partially cover it by a kT3 region as shown in the Fig. 7 and Fig. 8. The kT3 region can be covered by T3 tiles because of the induction hypothesis. The region not covered by the kT3 region is decomposed either in three parts, or four parts, according to k being even or odd. The decomposition for k even is shown in Fig. 7. The first two parts are parallelograms, (I) of dimensions (k+3, 3), and (II) of dimensions (k/2 -3, 3). Both of them can be covered by parallelograms of dimensions (3,1), which consists of four T3 tiles (see Fig. 7). The third part is of type 3T3, hence can be covered by T3 tiles as well. The decomposition for k odd is shown in Fig. 8. The first two parts are parallelograms, (I) of dimensions (k, 3), and (II) of sizes (k/2 - 3/2, 3). Both can be covered by parallelograms of dimensions (3,1). Part (III) is a equilateral triangle, with sides of length 3, and can be covered as in Fig. 8. Finally, the fourth part is of type 3T3.

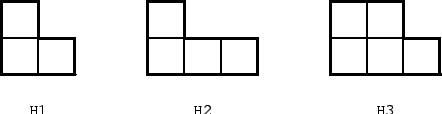
Figure 9

Figure 9:

There are three hexagons that can be dissected into four replicas (see Fig. 9). The first one is made out of three squares, the second one out of four squares, and the third one out of five squares. We will denote them by H1,H2, and H3, respectively.

Proposition 4:  All three hexagons H1, H2, H3, are rep-k2 tiles for any k ≥ 1.

Rep-tiles Revisited Proof. The proof is again done by induction, but here the length of the induction step is different for each type of tile.

Figure 9

Figure 10:

Proof for H1. We show cases k =2, 3 in Fig. 10. Then we prove that rep-k2 implies rep-(k+2)2. The proof depends on the congruence class modulo 3 of k. If k ≅ 0 (mod 3) the proof is done according to Fig. 11. We take a (k+2)H1 region and partially cover it by a kH1 region. The kH1 region can be covered by H1 tiles because of the induction hypothesis. The region not covered by the kH1 region is decomposed in seven parts: two rectangles (I) and (VII) of dimensions (2,k), two rectangles (II) and (VI) of dimensions (2,3), two rectangles (III) and (V) of dimensions (2, 2k-3), and the region (IV) of type 2H2. All rectangles can be covered by rectangles of dimensions (2,3), which in turn can be covered by two H2 tiles.

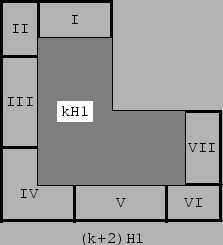
Figure 11

Figure 11:

If k ≅ 1 (mod 3) the proof is done according to Fig. 12. We take a (k+2)H1 region and partially cover it by a kH1 region. The kH1 region can be covered by H1 tiles because of the induction hypothesis. The region not covered by the kH1 region is decomposed in seven parts: two rectangles (I) and (VII) of dimensions (2, k-1), two rectangles (II) and (VI) of dimensions (2,3), two rectangles (III) and (V) of dimensions 2(2,2k-2), and the region (IV) of type 2H2. All rectangles can be covered by rectangles of dimensions (2,3), which in turn can be covered by two H2 tiles.

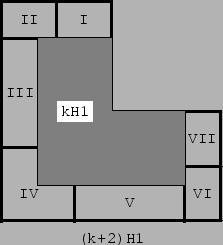
Figure 12

Figure 12:

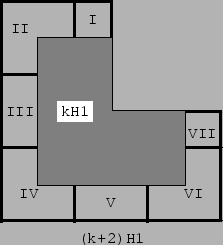
Figure 13

Figure 13:

If k ≅ 2 (mod 3) the proof is done according to Fig. 13. We take a (k+2)H1 region and partially cover it by a kH1 region. The kH1 region can be covered by H1 tiles because of the induction hypothesis. The region not covered by the kH1 region is decomposed in seven parts: two rectangles (I) and (VII) of dimensions (2,k-2), two rectangles (III) and (V) of dimensions (2,2k-4), and the regions (II), (IV), and (VI), of type 2H2. All rectangles can be covered by rectangles of dimensions (2,3), which in turn can be covered by two H2 tiles.

Figure 14

 

Figure 14:

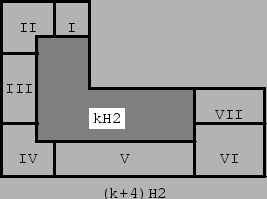
Figure 15

 

Figure 15:

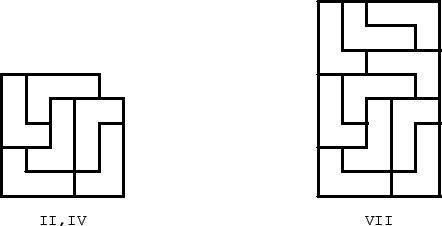
Figure 16

 

Figure 16:

Proof for H2. Observe that the proof is immediate if k is even. Indeed, if k is even, we can decompose kH2 in two rectangles of dimensions (2k,4k). Any such rectangle can be covered by rectangles of dimensions (2,4), which in turn can be covered by two H2 tiles (see Fig. 14). If k is odd, we proceed by induction. We already know cases k=2,4, and the case k=3 is dealt with in Fig. 14. We show that rep-k2 implies rep-(k+4)2. Take a (k+4)H2 region and partially cover it by a kH2 region as shown in the Fig. 15. The kH2 region can be covered by H2 tiles because of the induction hypothesis. The region not covered by the kH2 region is decomposed in seven parts: a rectangle (I) of dimensions (k-1,4), a rectangle (III) of dimensions (2k-2, 4), a rectangle (V) of dimensions (3k-1, 4), a rectangle (VI) of dimensions (k-1, 8), a rectangle (VII) of dimensions (5,8), and two squares, (II) and (IV), of dimensions (5,5) with a unit square missing in one of the corners. The rectangles (I),(III),(V), and (VI), can be covered by rectangles of dimensions (2,4), which consist of two H2 tiles, and the regions (II) and (IV), and the rectangle (VII), can be covered by H2 tiles as in Fig. 16.

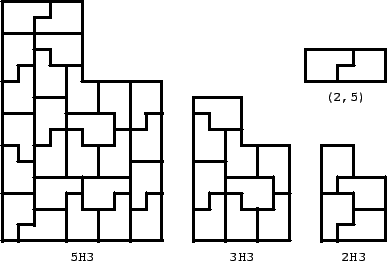
Figure 17

 

Figure 17:

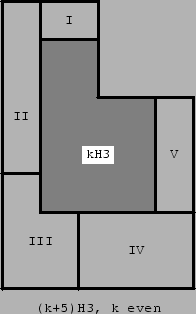
Figure 18

 

Figure 18:

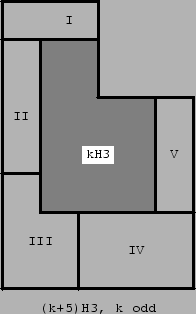
Figure 19

Figure 19:

Proof for H3. We show cases k=2,3,5 in Fig. 17. The case k=4 follows immediately from the case k=2. Then we prove that rep-k2 implies rep-(k+5)2. The proof depends on on the congruence class modulo 2 of k. If k ≅ 0 (mod 2), the proof is done according to Fig. 18. We take a (k+5)H3 region and partially cover it by a kH3 region. The kH3 region can be covered by H3 tiles because of the induction hypothesis. The region not covered by the kH3 region is decomposed in five parts: a rectangle (I) of dimensions (5,k), a rectangle (II) of dimensions (5,3k), a rectangle (IV) of dimensions (10,2k), a rectangle (V) of dimensions (5,2k), and the region (III) of type 5H3. The rectangles (I),(II),(IV), and (V) can be covered by rectangles of dimensions (2,5), which consist of two H3 tiles (see Fig. 17). If k ≅ 1 (mod 2), the proof is done according to Fig. 19. We take a (k+5)H3 region and partially cover it by a kH3 region. The kH3 region can be covered by H3 tiles because of the induction hypothesis. The region not covered by the kH3 region is decomposed in five parts: a rectangle (I) of dimensions (5, k+5), a rectangle (II) of dimensions (5, 3k-5), a rectangle (IV) of dimensions (10, 2k), a rectangle (V) of dimensions (5, 2k), and the region (III) of type 5H3. The rectangles (I),(II),(IV), and (V) can be covered by rectangles of dimensions (2,5), which consist of two H3 tiles.

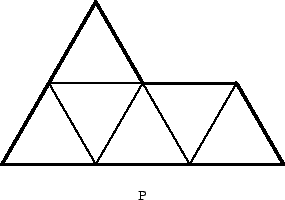
Figure 20

Figure 20:

There is a pentagon that can be dissected into four replicas (see Fig. 20). This figure is known as the "sphinx". It consists of five equilateral triangles. We will denote it by P.

Proposition 5   The pentagon P is rep-k2 tiles for any k ≥ 1.

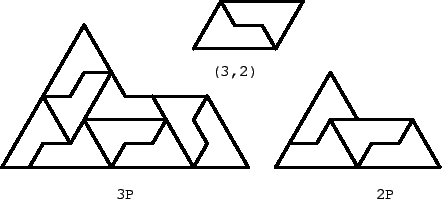
Figure 21

Figure 21:

Proof. We show cases k=2,3 in Fig. 21. Then we prove that rep-k2 implies rep-(k+3)2. The proof depends on the congruence class modulo 2 of k.

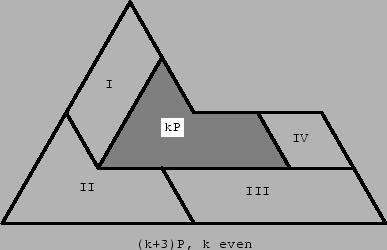
Figure 22

Figure 22:

If k ≅ 0 (mod 2), we take a (k+3)P region and partially cover it by a kP region as shown in the Fig. 22. The kP region can be covered by P tiles because of the induction hypothesis. The region not covered by the kP region is decomposed in four parts: a parallelogram (I) of dimensions (2k, 3), a parallelogram (III) of dimensions (3k,3), a parallelogram (IV) of dimensions (3,k), and the region (II) which is of type 3P. Parallelograms (I),(III) and (IV) can be covered by parallelograms of dimensions (2,3), which according to Fig. 21 can be covered by two P tiles.

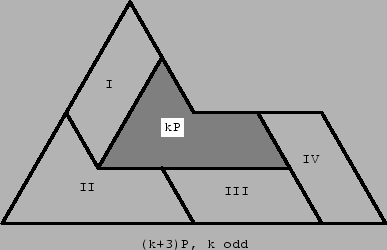
Figure 23

Figure 23:

If k ≅ 1 (mod 2), we take a (k+3)P region and partially cover it by a kP region as shown in the Fig. 23. The kP region can be covered by P tiles because of the induction hypothesis. The region not covered by the kP region is decomposed in four parts: a parallelogram (I) of dimensions (2k, 3), a parallelogram (III) of dimensions (3k-3, 3), a parallelogram (IV) of dimensions (3, k+3), and the region (II) which is of type 3P. Parallelograms (I),(III) and (IV) can be covered by parallelograms of dimensions (2,3), which can be covered by two P tiles.

Figure 24

Figure 24:

The last two convex polygonal rep-4 tiles we consider are obtained by changing slightly two of the tiles investigated so far. Note that H1 is being made out of three-fourths of a square. One can actually use here three-fourths of any rectangle (see Fig. 24). The new tile is also rep-k2for any k ≥ 1. The proof of this fact is similar with the proof for the hexagon H1, and we leave the details to the interested reader.

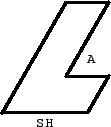
Figure 25

Figure 25:

Figure 26

 

Figure 26:

A more interesting modification is to take the second hexagon H2 and to skew it as in Fig. 25. The angle A is between 0 and Π. We will call the new tile SH (skewed hexagon). It is easy to see that SH is rep-k2 for any k even. Nevertheless, we believe that SH is not rep-k2 for any k odd. We hope to solve this question in a future article. Let us only mention here that this question is equivalent to the question of tiling kH2 using only translations (and no symmetries about the vertical or horizontal axis!) of the tiles shown in Fig. 26.

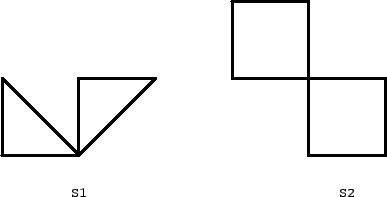
Figure 27

Figure 27:

There are two stellated polygons in the list, both shown in Fig. 27. We will denote them by S1 and S2. The proof of the following proposition is left as an exercise to the reader.

Proposition 6

  1. S1 is rep-k2 for any k ≥ 1;
  2. S2 is rep-k2 for any k even;
  3. S2 is not rep-k2 for any k odd.

Bibliography

  1. J. H. Conway and J. C. Lagarias: Tiling with polyominoes and combinatorial group theory J. Combin. Theory Ser. A 53 1990 183-208
  2. S. W. Golomb: Replicating figures in the plane Mathematical Gazette 48 1964 403-412
  3. M. Gardner: On "rep-tiles", polygons that can make larger and smaller copies of themselves Scientific American 208 1963 154-157
  4. I. Pak: Ribbon tile invariants Trans. AMS 352 2000 5525-5561
  5. W. P. Thurston: Conway's tiling groups Amer. Math. Monthly 97 1990 757-773

About this Document

Rep-tiles Revisited

This document was generated using the LaTeX2HTML translator Version 99.2beta8 (1.46)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were: 
latex2html reptiles.tex

The translation was initiated by Viorel Nitica on 2002-03-25